35 mm på aps-c och 50 mm på fullformat EXAKT samma?

[The_SuedeII]

Vänta nu, blandar vi (jag?) inte ihop två saker nu. Ska man inte separera på en bilds skärpedjup och en bilds "utseende".

En bilds utseende borde ju endast bero på bildvinkeln (och hur mycket som kommer med bestäms av avståndet och storleken på sensorn).
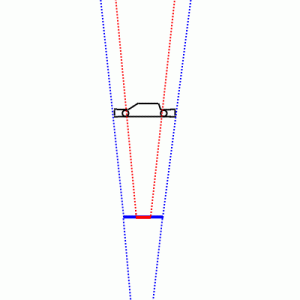
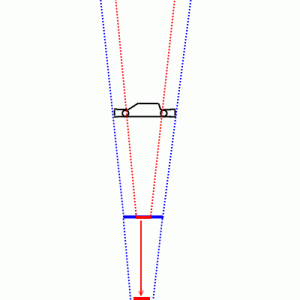
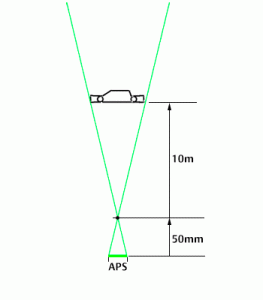
Antag jag står 10 meter ifrån tex en bil med en FF-kamera med 80 mm objektiv och bilen får precis plats på bilden.
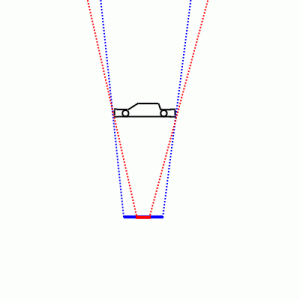
Står jag på samma plats med min APS-C med samma 80 mm objektiv får bilen inte plats i bilden. Men om jag backar bakåt tills bilen precis får plats i bilden - då borde ju utseendemässigt/innehållsmässigt de båda bilderna vara likadana!

Nej, som Melker sade ändras ju perspektivet drastiskt. Av bakgrunden (det som är bakom bilen) kommer det med mycket mer med FF än med APS på APS, trots att du fått backa till ca 15m med APS-kameran. Själva bilen kommer också ändras i perspektivförvrängning. Detta gör ganska mycket skillnad för utseendet på bilden.

Däremot skärpedjupet i en bild bestäms väl endast av avståndet till objektet samt den FYSISKA bländaröppningen.

Bara om du helt ignorerar bildens förstoringsgrad. Vilket är samma sak som att säga att det kvittar om du använder ett 20mm eller ett 200mm objektiv för att ta en bild. Vilket ju inte riktigt stämmer i praktiken. Oskärpan i OBJEKTETS mening däremot stämmer med vad du säger, mängden oskärpa mätt i cm eller dm på ett verkligt objekt framför dig bestäms av avstånd och frontpupill. Om ett mönster som är 10cm stort och 10m bakom skärpeplanet blir utblurrat bestäms av detta. Men om ett 20mm objektiv avbildar detta som kanske 5 pixlar i blurrning kommer 200mm avbilda det som 50 pixlar i blurrning. Vilket är ganska mycket synlig skillnad.

Vi använder samma exempel som ovan.
Jag står 10 meter från en bil med min FF-kamera och 80 mm objektiv med f/5.6 bländare. Jag får då ett visst skärpedjup och en viss bildvinkel.
Jag står kvar på samma plats men byter till en APS-C kamera med 50 mm objektiv och ställer in f/3.5 bländare. Då ska jag få EXAKT samma skärpedjup som med min FF. Men! Bildvinkeln blir INTE samma, den blir större och tar med mer av bakgrunden och bilderna är inte längre utseendemässigt/innehållsmässigt likadana.

Stämmer ovanstående resonemang?

Nej. De ger väldigt, väldigt liknande resultat, även i verkligheten. Det är bara att prova - vilket du uppenbarligen inte gjort, för då hade du inte skrivit detta...

Att faktiskt ifrågasätta "kunskap" och prova den i verkligheten är något av det nyttigaste man kan göra.

 

[The_SuedeII]

Det roliga med det sista, ekvivalens-regeln som ger 80F5.6 och 50F3.5, är att om du har samma slutartid kommer även bruset bli väldigt lika.

Där kommer nästa sak som kan vara en "Aha!"-upplevelse, nämligen att brus som funktion av slutartid bestäms av skärpedjupet... Det är därför FF-kameror brusar mindre på ett visst ISO än vad APS-kameror gör. I slutänden om man går alla de optiska/fysiska ekvationerna runt, hela cirkeln (allt hänger ju ihopa!) är [bildbruset per slutartid] lika med [skärpedjupet ^-1]....

Mer skärpedjup, samma slutartid = mer brus!

 

[Rommel]

Den sista ekvationen gäller klart enbart om sensorn har likvärdiga egenskaper!

 

[Henrik-J]

Tackar för all feedback!

Du var nästan rätt The_Suedell - jag har provat detta i verkligheten men sedan började jag fundera på teorin och nu får jag inte teori och praktik att stämma (praktiken fungerar men inte teorin). Jag gillar inte när dessa två inte överensstämmer.

Eftersom jag varit rejält förkyld och febrig de senaste dagarna har jag haft många timmar över till funderande


Här är min teori beskriven med figurer. Uppenbarligen måste det alltså finnas någon rejäl tankevurpa här någonstans - kan ni hjälpa mig att hitta var?


Utgångpunkten (första figuren)
Står 10 meter ifrån en bil. Både FF och APS-C kameran har ett 80 mm objektiv.
Det blåa strecket motsvarar en FF kameras sensor, det röda en APS-C kameras sensor.
Bildvinkeln, som bestäms av objektivet, visas med de streckade linjerna.
Det APS-C sensorn fångar upp är ju i princip bara ett utsnitt av vad FF sensorn fångar upp, vilket illustreras i figuren nedan.
So far so good - eller hur?


Backa tillbaka (andra figuren)
Det är nu jag började tänka - hur gör en APS-C för att få med samma innehåll i bilden som en FF?
Om han backar tillbaka med sin APS-C sensor precis som figuren nedan så borde ju innehållet i bilden bli samma som för FF i exemplet "Utgångspunkten"?
Fast jag inser nu att både perspektiv och innehåll framför bilen borde bli annorlunda. Men innehållet bakom bilen borde väl åtminstonde vara samma?


80 v 50 mm (tredje figuren)
Ok, vi använder samma exempel igen - fast denna gången använder APS-C kameran ett 50 mm objektiv istället!
Då tycker jag att bildvinklarna borde bli på följande sätt. Ett 80 mm objektiv har ju en snävare bildvinkel än ett 50 mm objektiv.
När jag tittar på andra figuren nedan så får ju båda kameror med lika mycket av huvudmotivet. Men! APS-C kameran verkar ju få med mycket mer av bakgrunden!

 

[ErlandH]

Bildvinkeln, som bestäms av objektivet, visas med de streckade linjerna.
Det APS-C sensorn fångar upp är ju i princip bara ett utsnitt av vad FF sensorn fångar upp, vilket illustreras i figuren nedan.
So far so good - eller hur?

Nej, du tänker o ritar fel. Utsnittet innebär att bildvinkeln förändras. Röda o blå linjer ska inte vara parallella. Om hälften av bilden skärs bort vid sensorn skärs också hälften bort tio meter från kameran.

 

[The_SuedeII]

Perspektivet rör sig alltid runt en fast punkt, det optiska centrumet av det plan där frontpupillen är. Mitt i bländaren alltså, där bländaren SER UT att sitta om man tittar in i objektivet framifrån. Linjerna "ut" från objektivet med två olika sensorstorlekar blir alltså inte parallella ut från sensors kanter, som i dina i övrigt jättefina illustrationer , de passerar/korsar oavsett sensorstorlek alltid genom denna punkt. Oftast ser man detta helt felaktigt (oftast också av panorama-människor) benämnt som "den främre nodalpunkten".

Häri ligger nog felet i ditt geometriska "tänk".

 

[Rommel]

1 5D 50mm hur mycket fås med
https://dl.dropboxusercontent.com/u/3697094/1 5D.jpg

2 5D 50mm, bokeh
https://dl.dropboxusercontent.com/u/3697094/2 5D.jpg

3 EOS M 35mm (motsvarar 56mm) hur mycket fås med
https://dl.dropboxusercontent.com/u/3697094/3 EOS M.jpg

24 EOS M 35mm,(motsvarar 56mm) bokeh
https://dl.dropboxusercontent.com/u/3697094/4 EOS M.jpg

Alla på stativ, samma inställningar, samma bildbehandling via LR. Dvs obefintlig.

/stefan

 

[Henrik-J]

Perspektivet rör sig alltid runt en fast punkt, det optiska centrumet av det plan där frontpupillen är. Mitt i bländaren alltså, där bländaren SER UT att sitta om man tittar in i objektivet framifrån. Linjerna "ut" från objektivet med två olika sensorstorlekar blir alltså inte parallella ut från sensors kanter, som i dina i övrigt jättefina illustrationer , de passerar/korsar oavsett sensorstorlek alltid genom denna punkt. Oftast ser man detta helt felaktigt (oftast också av panorama-människor) benämnt som "den främre nodalpunkten".

Häri ligger nog felet i ditt geometriska "tänk".

Nu får jag ingen teori att gå ihop - dessutom är det inte omöjligt att jag använder tekniska termer som jag inte riktigt behärskar, nu har vi optiska centrum, frontpupiller och nodalpunkter.

Brännvidden - kanske bäst att börja med det. Det här är min uppfattning av brännvidd för en helt vanlig konvex lins (en bild jag hittat på nätet) - se figure nedan. Det är helt enkelt avståndet från centrum av linsen till punkten där parallellt infallande ljusstrålar möts i en punkt.
Anta nu att jag har en konvex lins med brännvidden 80 mm och en annan med brännvidden 50 mm.

Sensor - enkelt. Jag har en sensor som är 24x36 mm (FF) och en som är 22.2x14.8 mm (APS-C).

Så vad är nästa logiska steg härifrån? Hur förklarar man bildvinkel och vad som kommer med i bilden och inte kommer med i bilden med ovanstående fyra komponenter och lite ljusstrålar?

 

[PMD]

Perspektivet rör sig alltid runt en fast punkt, det optiska centrumet av det plan där frontpupillen är.

Joakim! Det där är en av de bättre illustrationerna jag har sett för att visa på skillnader och likheter mellan två olika bildformat. Mycket pedagogiskt.

 

[Henrik-J]

Joakim! Det där är en av de bättre illustrationerna jag har sett för att visa på skillnader och likheter mellan två olika bildformat. Mycket pedagogiskt.

Men varför flyttar sig sensorplanet? Utgångspunkten var ju att kameran skulle vara på samma ställe. Hänger inte riktigt med på den figuren.

 

[PMD]

Sensorplanets avstånd till objektivets optiska centrum är olika för objektiv med olika brännvidder. Det är ju själva definitionen av brännvidd.

 

[Henrik-J]

Sensorplanets avstånd till objektivets optiska centrum är olika för objektiv med olika brännvidder. Det är ju själva definitionen av brännvidd.

Njae.... Det låter inte rimligt - brännvidden är definerat enbart av linsen/linserna. Ta en vanlig konvex lins vars brännvidd är definerad utan någon referens till något sensorplan.

Se figur nedan för definition av brännvidd.


Däremot om man placerar den här konvexa linsen så att avståndet mellan dess center och sensorplattan är precis dess brännvidd - då har man ställt in fokus för att fokusera mot oändligheten.

 

[The_SuedeII]

Men varför flyttar sig sensorplanet? Utgångspunkten var ju att kameran skulle vara på samma ställe. Hänger inte riktigt med på den figuren.

Kom ihåg att det är inte KAMERAN som är den optiska centerpunkten i systemet, det är objektivet.

Varför flytta? -Därför att om APS-kameran står på exakt 10m avstånd från sensorplan till motiv måste man antagligen flytta 30mm längre bak (till 10m 3cm) med FF-kameran för att objektivets ingångspupill ska vara på samma ställe. Och återigen - det är ingångspupillen som bestämmer perspektivets rotationspunkt, inte kameran.

80mm på FF, 50mm på APS >>> kameran ska 30mm längre bak.

 

[The_SuedeII]

Njae.... Det låter inte rimligt - brännvidden är definerat enbart av linsen/linserna. Ta en vanlig konvex lins vars brännvidd är definerad utan någon referens till något sensorplan.

Se figur nedan för definition av brännvidd.
[---]
Däremot om man placerar den här konvexa linsen så att avståndet mellan dess center och sensorplattan är precis dess brännvidd - då har man ställt in fokus för att fokusera mot oändligheten.

Ett objektiv är ju ett fokuserande system, dvs summan av alla ingående element måste bli positiv (konvex, samlande). Brännvidden är avståndet från sensorplanet fram till den bakre principalpunkten (när objektivet är fokuserat på oändlighet!). Förenklat till en "thin-lens" som i våra schematiska exempel blir både in- och utgångspupillen representerad av bländaren, mitt i objektivet.

Det finns en bra sammanfattning, halvdjup, på:
http://photo.net/learn/optics/lensTutorial

Vill man gräva djupare rekommenderar jag:
"Applied Photographic Optics" av Sidney Ray

 

[Henrik-J]

Kom ihåg att det är inte KAMERAN som är den optiska centerpunkten i systemet, det är objektivet.

Varför flytta? -Därför att om APS-kameran står på exakt 10m avstånd från sensorplan till motiv måste man antagligen flytta 30mm längre bak (till 10m 3cm) med FF-kameran för att objektivets ingångspupill ska vara på samma ställe. Och återigen - det är ingångspupillen som bestämmer perspektivets rotationspunkt, inte kameran.

80mm på FF, 50mm på APS >>> kameran ska 30mm längre bak.

Ok, det börjar klarna lite nu. Har suttit och skissat och funderat en del.

Fast jag vet inte vad optisk centerpunkt betyder, ej heller ingångspupill.

Det är väl skalan som är lite missledande kanske. Vår utgångspunkt var att du ska kunna stå på samma plats med FF+80 och APS+50 och få samma bildinnehåll. Därför blev jag tveksam när plötsligt sensorplanet började röra på sig kraftigt. Men det visar sig att det var ganska små rörelser

Jag har dock läst på lite hur man beräknar bildvinkeln. Har alltid läst att bildvinkeln endast bestäms av linsens brännvidd och sensorns storlek - men det verkar bara vara en approximation som fungerar fint så länge som avståndet till motivet är mycket större än avståndet mellan linsens centrum och sensorplanet.

EDIT : Allt vi diskuterar måste väl rimligtvis kunna förklaras med en enda vanlig konvex lins? Skulle underlätta, så man slipper alla de här ingångar, utgångar, pupiller, principalpunkter både fram och bak

 

[PMD]

Ok, det börjar klarna lite nu. Har suttit och skissat och funderat en del.

Fast jag vet inte vad optisk centerpunkt betyder, ej heller ingångspupill.

Förenkla resonemangen genom att approximera objetiven med en tunn lins, som Joakim föreslog. Då blir all geometri och alla formler man kan härleda ur geometrin mycket enklare. Om man inte börjar med att blanda in begrepp som in- och utgångspupiller, principalpunkter, nodalpunkter etc, så blir allting mycket lättare att begripa och man kan snabbare få en förståelse för hur optik fungerar. Sen kan man läsa på om lite mer avancerade konstruktioner.

Börja här, t.ex.

 

[Henrik-J]

Förenkla resonemangen genom att approximera objetiven med en tunn lins, som Joakim föreslog. Då blir all geometri och alla formler man kan härleda ur geometrin mycket enklare. Om man inte börjar med att blanda in begrepp som in- och utgångspupiller, principalpunkter, nodalpunkter etc, så blir allting mycket lättare att begripa och man kan snabbare få en förståelse för hur optik fungerar. Sen kan man läsa på om lite mer avancerade konstruktioner.

Börja här, t.ex.

Nu missade du nog lite historik i tråden. Jag har alltd bara pratat om en enkel konvex lins, se tex mitt inlägg #48, just för att hålla det enkelt.

Alla mina frågor och försök till härledning och förståelse handlar om en enkel konvex lins.

Kommer lite senare idag lägga upp en skiss som i princip är som Joakim's fast jag har lagt till en konvex lins, lite mått på bildvinkel och brännvidd. Det är just brännvidden jag skulle vilja ha in i figuren också.

 

[PMD]

Brännvidden är med i Joakims bild. Det är avståndet mellan linsen och sensorplanet; 50mm i APS-C-fallet och 80mm i småbildsfallet ("FF").

Eftersom linsen är fokuserad på ett motiv som befinner sig 10m framför linsen så är det inte helt korrekt med ovanstående, men 10m är tilräckligt nära oändligheten för att det ska vara ungefär rätt. Ju längre bort motivet är desto bättre stämmer det. I länken jag föreslog i inlägg #56 finns ett avsnitt om avbildning som ger en formel som är mer i överensstämmelse med verkligheten.

 

[ErlandH]

Sensor - enkelt. Jag har en sensor som är 24x36 mm (FF) och en som är 22.2x14.8 mm (APS-C).

De övningar som pågår nu i tråden är säkert intressanta, men Henriks tankevurpa är ju enklare än så och syns tydligt redan i figur ett i #44.

Om ff-sensorn är 36 mm bred och den andra bara 22 mm så innebär det att det är 7 mm (20 procent) på varje sida som skärs bort vid sensorplanet, om man står på samma punkt och använder samma objektiv.

Vi säger att motivet är en bil som är 5 meter lång och helt fyller bildens bredd med ff-sensor. Enligt Henriks figur ett är det bara 7 mm av bilens ytterändar som inte kommer med i bilden med aps-c-sensorn. I verkligheten är det dock 20 procent i varje ände (dvs 1 meter) av bilen som skärs bort, eftersom bildvinkeln blir en helt annan.

De röda och blå linjerna i figur ett ska INTE vara parallella.

 

[The_SuedeII]

Ok, det börjar klarna lite nu. Har suttit och skissat och funderat en del. Fast jag vet inte vad optisk centerpunkt betyder, ej heller ingångspupill.

Bry dig inte på det, det är ganska (väldigt!) många steg längre fram i förståelsen. Båda två kan dock förenklas ner till centrumet i modellen "tunn lins".

Det är väl skalan som är lite missledande kanske. Vår utgångspunkt var att du ska kunna stå på samma plats med FF+80 och APS+50 och få samma bildinnehåll. Därför blev jag tveksam när plötsligt sensorplanet började röra på sig kraftigt. Men det visar sig att det var ganska små rörelser

Jupp, 10 meter på ena sidan, och mått i millimeter på andra sidan. Schemat var inte direkt skalenligt, men det är ju inte bilen jmf sensorn heller för den delen...

Jag har dock läst på lite hur man beräknar bildvinkeln. Har alltid läst att bildvinkeln endast bestäms av linsens brännvidd och sensorns storlek - men det verkar bara vara en approximation som fungerar fint så länge som avståndet till motivet är mycket större än avståndet mellan linsens centrum och sensorplanet.

Det fungerar fint väldigt långt ner i avstånd. "Mycket större" innebär låga felmarginaler ner till 10-20x och det är väldigt nära. En meter avstånd med ett 50mm-objektiv är ju 20x. Eller egentligen 19x, eftersom de "20" delas på 19 framför och 1 bakom...

EDIT : Allt vi diskuterar måste väl rimligtvis kunna förklaras med en enda vanlig konvex lins? Skulle underlätta, så man slipper alla de här ingångar, utgångar, pupiller, principalpunkter både fram och bak

Det är precis vad som är gjort. Det du fortfarande antagligen inte gör rätt i huvudet är att korsa linjerna i den konvexa linsen. Bilden som projiceras/fokuseras på sensorn är spegelvänd och upp och ner.