Jag räknar inte riktigt som DSPographer, som för övrigt har mycket vettigt att säga - om man har vett att sortera det. Här har han dock vänt lite på siffrorna... För att nyquist ska ha en chans att arbeta ska man dubbla mängden samples, inte halvera dem som han gör. Och det är dessutom onödigt...

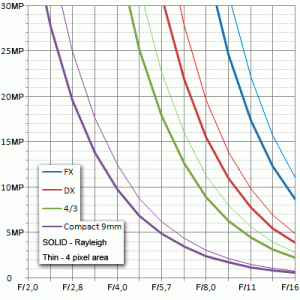
Rayleigh (för grönt ljus) är som skrivs 1.22x0.55xFtal µm
Pixelpitch (c-c mått) är i x- och y-led ganska exakt storleken genom upplösningen:
22.3mm/5230pixlar = ~4.25µm - Jag har lagt till 50 pixlar, dom finns alltid där men används inte. Man drar dock inte av för dem när man räknar storleken på sensorn...

Sen ska man lägga till effekten av AA-filtret (litet) och färgfiltret (stort).
Enklast är att räkna på en svart linje på en vit bakgrund, här finns alla färger representerade.
Jag tycker han gör fel som räknar diagonaler, man kan se/mäta verklig påverkan redan vid raka x- och y-led - även om dessa pixlar inte har samma färgfilter framför sig på sensorn. Då hamnar man på:
1.22x0.55x(Ftal) = 4.25x(förlustfaktorn för AA och färgfilter)
>
Ftal = (4.25x(1.2?)) / (1.22x0.55) = 7.6
Vid F/7.6 (F/8 då!) är det alltså möjligt att SE och MÄTA en diffraktionsförlust med en tydlighet som inte kan misstolkas - om man vet att objektivet inte har några andra dumheter för sig.
Men jag är ganska säker på att man måste upp på F/11 för att få direkt störiga effekter (direkt, synbar kontrastförsämring) ens vid 100% på skärm.
Vid undersökningar bl.a på Fraunhofer har man kunnat påvisa att en "4-pixel-area" av diffraktion hjälpligt går att skärpa upp med förskärpningen i raw-omvandlaren eller med algoritmer som Richardson-Lucy eller bara Smart-sharpen (accurate) i Photoshop. Man förlorar en del detaljering, men vid normala utskrifter/påsynsstorlekar på skärm är skillnaden inte direkt störande - efter att efterbehandlingen gjort sitt!