maxzomborszki
Aktiv medlem
Annat ämne egentligen, skärpedjup och "1/3 + 2/3 tumregeln"
Detta stämmer bara för ett visst fokusavstånd. Vanligtvis brukar skärpedjupet beräknas med följande formler. Först beräknar man hyperfokalavståndet:
H = (f * f) / (A * c)
Där f är fokallängden, A är bländarvärdet och c är den sk "circle-of-confusion" för det aktuella filmformatet. För 35mm-film brukar man ofta använda 0,033mm.
Därefter kan man räkna ut närgränsen för skärpedjupet som:
NF(s) = (H * s) / (H + (s - f))
Där s är avståndet till motivet. På samma sätt fås den bortre gränsen för skärpedjupet som:
FF(s) = (H * s) / (H - (s - f))
Dessa formler fås ur geometri av strålgången genom objektiv. Nicholas Sushkin har en bra sida (http://www.dof.pcraft.com/) som förklarar detta. Dock så använder han andra formler, Df och Dr, istället för NF respektive FF. Dessa värden är inte närgränsen utan avståndet från närgränsen till fokusavståndet, dvs NF = s - Df och FF = s + Dr.
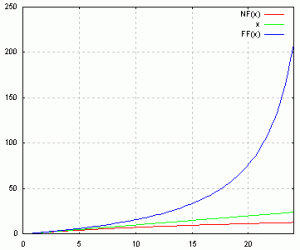
Antag att vi har ett 50mm objektiv och använder bländare 2.8. Då har blir, med ovanstående formler och värden, hyperfokalavståndet ca 27 meter. (Det tog en liten stund att skriva det här inlägget för jag var tvungen att lära mig gnuplot så jag kunde göra nedanstående graf.) De tre kurvorna visar näravståndet NF(s), fokusavståndet s och den bortre gränsen FF(s) och skalan är i meter. Jag plottade bara till 24 meter för sedan sticker den bortre gränsen iväg mot oändligheten och då blir skalorna så absurda på grafen. Som man ser så är det vid ett avstånd som 1/3 + 2/3-regeln gäller, efter okulär inspektion av grafen borde det vara runt ca 9 meter. Bortanför detta så skiljer det sig mer, framför detta avstånd så går det mot mer lika delar framför och bakom.
Inte för att det spelar så jättestor roll egentligen men jag tycker det är synd att man lär ut denna typ av "absoluta sanningar" som folk går efter. Bättre vore att lära ut att skärpedjupet är inte lika stort framför som bakom. Ju längre bort du fokuserar desto större blir skillnaden och mer inkluderas bakom.
En intressant diskussion när man kommer till detta är de som inte tycker att hyperfokalavståndet är så mycket att fästa sig vid. Det är ju nämnligen så att när man fokuserar på hyperfokalavståndet så är det ofta för att man vill ha så stort skärpedjup som möjligt. Dessa motståndares argument går ut på att då är ofta det som är oändligt långt borta, landskapet vid horisonten intressant. Men detta ligger ju på gränsen till vad som är oskarpt genom att man räknar med att detaljer där kommer avbildas med en storlek motsvarande "circle-of-confusion". Om det nu är det som är viktigt så bör man kanske fokusera lite bortanför hyperfokalavståndet och leva med att förgrunden blir lite suddigare i förstoringarna. Så även om man med matematik kan räkna på strålgången (notera att verkligheten är inte lika exakt) så måste man ändå tolka resultaten efter de egna behoven.
Är det någon som hittar något fel i mina beräkningar så är jag tacksam om ni påpekar detta för mig. Det var bara någon vecka sedan jag fann länken jag presenterade först och där fick jag mig en tankeställare som visade sig överensstämma med den optik jag lärt mig en gång och krockade med den 1/3 + 2/3-regel som jag också fick lära mig en gång i tiden. Det är inte fel att vara kritisk samt våga ifrågasätta, även mot detta inlägg
Plåta nu, inte plotta.
Fina sidor men jag reagerade lite över "Bra att veta är att skärpedjupet fördelar sig så att 1/3 av totala skärpedjupet hamnar framför motivet och 2/3 bakom. Skärpedjupet är alltså dubbelt så stort bakom motivet som framför." på sidan om objektiv. Det gäller inte alltid. Se gärna "Common misperceptions" på http://members.aol.com/Photoinfo/dof.html.RawBeer [E.F.S] skrev:
http://www2.skolor.pedc.se/franssuell/FOTO/teknik.html
Detta stämmer bara för ett visst fokusavstånd. Vanligtvis brukar skärpedjupet beräknas med följande formler. Först beräknar man hyperfokalavståndet:
H = (f * f) / (A * c)
Där f är fokallängden, A är bländarvärdet och c är den sk "circle-of-confusion" för det aktuella filmformatet. För 35mm-film brukar man ofta använda 0,033mm.
Därefter kan man räkna ut närgränsen för skärpedjupet som:
NF(s) = (H * s) / (H + (s - f))
Där s är avståndet till motivet. På samma sätt fås den bortre gränsen för skärpedjupet som:
FF(s) = (H * s) / (H - (s - f))
Dessa formler fås ur geometri av strålgången genom objektiv. Nicholas Sushkin har en bra sida (http://www.dof.pcraft.com/) som förklarar detta. Dock så använder han andra formler, Df och Dr, istället för NF respektive FF. Dessa värden är inte närgränsen utan avståndet från närgränsen till fokusavståndet, dvs NF = s - Df och FF = s + Dr.
Antag att vi har ett 50mm objektiv och använder bländare 2.8. Då har blir, med ovanstående formler och värden, hyperfokalavståndet ca 27 meter. (Det tog en liten stund att skriva det här inlägget för jag var tvungen att lära mig gnuplot så jag kunde göra nedanstående graf.) De tre kurvorna visar näravståndet NF(s), fokusavståndet s och den bortre gränsen FF(s) och skalan är i meter. Jag plottade bara till 24 meter för sedan sticker den bortre gränsen iväg mot oändligheten och då blir skalorna så absurda på grafen. Som man ser så är det vid ett avstånd som 1/3 + 2/3-regeln gäller, efter okulär inspektion av grafen borde det vara runt ca 9 meter. Bortanför detta så skiljer det sig mer, framför detta avstånd så går det mot mer lika delar framför och bakom.
Inte för att det spelar så jättestor roll egentligen men jag tycker det är synd att man lär ut denna typ av "absoluta sanningar" som folk går efter. Bättre vore att lära ut att skärpedjupet är inte lika stort framför som bakom. Ju längre bort du fokuserar desto större blir skillnaden och mer inkluderas bakom.
En intressant diskussion när man kommer till detta är de som inte tycker att hyperfokalavståndet är så mycket att fästa sig vid. Det är ju nämnligen så att när man fokuserar på hyperfokalavståndet så är det ofta för att man vill ha så stort skärpedjup som möjligt. Dessa motståndares argument går ut på att då är ofta det som är oändligt långt borta, landskapet vid horisonten intressant. Men detta ligger ju på gränsen till vad som är oskarpt genom att man räknar med att detaljer där kommer avbildas med en storlek motsvarande "circle-of-confusion". Om det nu är det som är viktigt så bör man kanske fokusera lite bortanför hyperfokalavståndet och leva med att förgrunden blir lite suddigare i förstoringarna. Så även om man med matematik kan räkna på strålgången (notera att verkligheten är inte lika exakt) så måste man ändå tolka resultaten efter de egna behoven.
Är det någon som hittar något fel i mina beräkningar så är jag tacksam om ni påpekar detta för mig. Det var bara någon vecka sedan jag fann länken jag presenterade först och där fick jag mig en tankeställare som visade sig överensstämma med den optik jag lärt mig en gång och krockade med den 1/3 + 2/3-regel som jag också fick lära mig en gång i tiden. Det är inte fel att vara kritisk samt våga ifrågasätta, även mot detta inlägg
Plåta nu, inte plotta.