Mycket intressant, detta är en av de saker jag funderat över ett tag, skulle du kunna utveckla det mer? Jag antar att bländaren (antal lameller och form) har en viss inverkan (går det föresten att beskriva just den lite mer än den gängse beskrivningen; hård/mjuk?
Vad är det föresten i nikons defocus control objektiv som faktiskt kan justeras med den inre ringen? Alltså 105/2,0DC respektive 135/2,0DC om de är bekanta i sammanhanget.
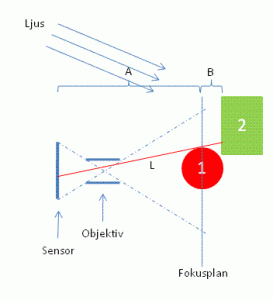
Bländaren påverkar på så sätt att oskärpehets-"cirkeln" får samma form som bländaren (i alla fall i bilden mitt, utåt hörnen blir det sedan oftast lite deformerat åt ellipshållet av optiska skäl samt att vinjettering på stora bländare kan göra att andra saker än bländaren skärmar av ljuset och därför bestämmer formen).
Det som bär huvudansvaret för bokehns karaktär ifråga om hård/mjuk är dock inte formen utan att ljuset är ojämnt fördelat inom "cirkeln" på grund av olika linsfel (i mitten är det i synnerhet sfärisk aberration). Är cirklarna ljusast i mitten och mörknar utåt blir bokehn "mjuk" och är de istället mörkare i mitten och har ljus rand blir den "hård".
Det som justeras i Nikonobjektiven i fråga är helt enkelt graden av korrektion av i huvudsak sfärisk aberration.
Det bör också tilläggas att när denna linsfelsrelaterade bokeh är mjuk i bakgrunden så är den hård i förgrunden och vice versa, oftast är det ju dock bakgrundsoskärpan vi är mest intresserade av.
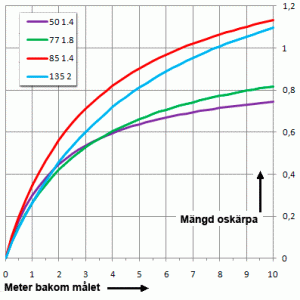
När vi sedan fokuserar på olika avstånd påverkar vi linsfelen (antingen genom eventuella inre förändringar av linsavstånden men även förändringen av avbildningsskalan i sig påverkar linsfelen ganska mycket på stora bländare). Bokehn kan därför genomgå ganska stora förändringar beroende på avstånden även om de inbördes förhållandena mellan huvudmotiv och bakgrunden råkar ge lika stora oskärepehetscirklar.
Ofta är dessutom oskärpehetscirkelns inre ljusfördelning så ojämnt fördelad att den t.ex är ljus i mitten för att sedan först avta innan den blir ljusare igen längst ut i periferin (vanligt inte minst med ljusstarka objektiv). Bländar man nu ner ett sådant här objektiv så är det den ljusa randen som först försvinner vilket gör att bokehn förändras radikalt från hård på full öppning till påtagligt mjuk ett eller två steg nerbländat (priset för detta är naturligtvis att oskärpehetscirklarna blir mindre och bakgrunden därför inte lika oskarp).
När du skriver relativa, så avser det alltså hela sensorn eftersom den absoluta skall delas med diagonalmåttet? Vore det inte också intressant att jämföra det med pixelytan? (när den absoluta oskärpecirkeln är mindre än pixelytan (jag bortser från bayerfiltret här) så borde det ju inte kunna bli skarpare?
När vi talar oskärpa, eller i alla fall är i närheten av skärpedjupsgränsen, så är oskärpehetscirklarna mycket större än pixlarna att det är rätt uppenbart att de förra dominerar. Ser vi saken ytmässigt så utgör en cirkel på 0,02 mm en knapp miljondel av en APS-sensor, d.v.s den är en tiopotens större än en pixel av idag.
Samspelet när det handlar om skärpa, d.v.s. när våra cirklar och pixlar är i samma storleksordning, är inte lika enkelt att avfärda. Det viktiga i sammanhanget är att ljusets fas försvinner när ljuset registreras på sensorn och det gör att MTF-värdet för objektivet (inklusive våra små cirklar) och MTF-värdet för sensorn (inklusive bayermönster och AA-filter) helt enkelt bara behöver multipliceras för att få det totala MTF-värdet. Att mäta upp MTF-värdena för objektiv och sensor var för sig är den svåra delen, när man gjort det har man dock avslöjat alla hemligheter (man kan säga att det finns ett slags vattentätt skott mellan objektiv och sensor på grund av att ljusets fasinformation försvinner när det registreras, detta gör att vi kan behandla objektiv och sensor som två av varandra helt fristående delar).