Få ut mer av Fotosidan som inloggad
Fotosidan är gratis! Som inloggad får du smarta funktioner. Du kan ladda upp 10 bilder och få kritik på dem. Du får vårt nyhetsbrev. Du kan skapa köp&sälj annonser mm

Merläsning
Annons
Så förenklar och effektiviserar AI vardagen för fotografer
Annons
Som fotograf eller videograf vet du att kreativiteten ofta kommer när du minst anar det – på väg till en location, i bilen efter ett kundmöte, eller mitt under en plåtning när ljuset faller på ett sätt du inte förväntat dig. Men i ett yrke där fokus ligger på att fånga ögonblick, är det lätt att egna tankar, bildidéer eller feedback från kunden glöms bort.
Läs mer...





















31 Kommentarer
Logga in för att kommentera
/Maverick
Jag brukar förenkla gyllene snittet till att dela in bildytan i tre lika stora delar, både på längden och bredden, och i en eller flera av de bildade skärningspunkterna placera det som ska tilldra sig intresset i en bild. Inte så vetenskapligt men ganska effektivt...
Intressant med gyllene snittet för man finner det på så många sätt i naturen, t.ex en spiralsnäcka
Panthenon eller vad det nu heter är byggd efter principen ovan, det var oerhört intressant, de har byggt kolossen runt och vint, har för mig att det kallas optisk synvilla, dvs en betraktare på en viss punkt ska kunna se det optimala panthenon.
Fast när man synar byggnaden närmare ser man att inget är rakt...
Alla hus runt om är placerad noggrant för att upphöja bilden av panthenon.
Detta visades i Discovery för inte så länge sedan...
Skulle önska ett mer praktiskt inriktad artikel.
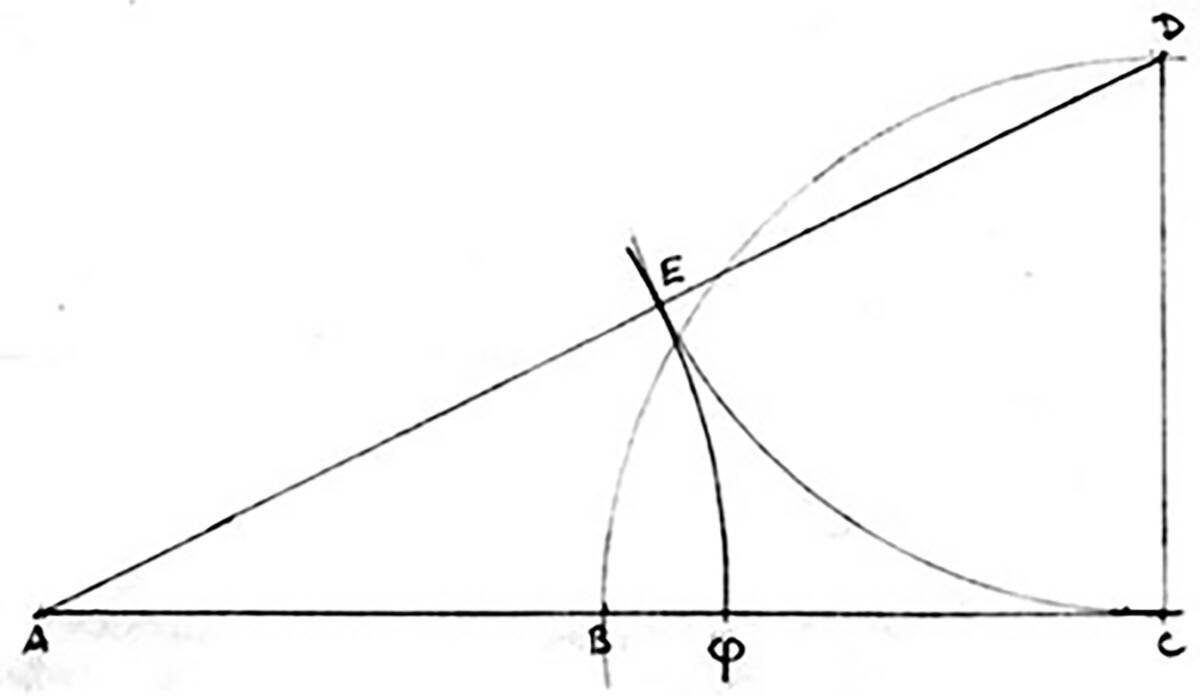
AGFC är en gyllene rektangel.
Förresten vad då gyllene?
ABCD är ingen kvadrat. ABDC är en kvadrat.
Ändå bättre är att dela sträckan i fem lika delar. Då ligger det Gyllene snittet nära delningen av sträckan i förhållandet två till tre.
Andra delningar är:3:5, 5:8. 8:13, 13:21 osv.
Det är Fibonaccis talserie 1/2, 2/3, 3/5, 5/8, 8/13, 8/21.. som konvergerar mot det Gyllene snittet
Om inte, fan va dumt!
Massor av exempel här:
http://bildburen.blogspot.com/
/Ingemar E
Matematik är ett språk.
Pytagoras, och kanske framför allt Euklides, beskrev hur olika proportioner förhöll sig. Bokstavligt handlar det om hur man delar en linje av en viss längd på det mest harmoniska vis som går... Frågan är om det gyllene snittet är verklighet eller inte... men de lyckades skapa en matematisk dikt som har fascinerat eftervärlden. Så enkel, så exakt, så expanderbar. Dikten beskriver vår omvärld med precis den exakthet, eller brist där av, som gör att man undrar om det är sant eller inte... Förnära för att vara lögn. Lite för avvikande för att vara absolut sanning. Tveklöst matematisk vacker prosa.
Pytagoras och Euklides efterföljare har utvecklat teorin in absurdum... Det har tidvis till och med varit ett gudomligt teorem! (För att kontra Skenbild:s lallande om ”ramverk”. Skenbild hade bränts på bål under medeltiden... ;0))!
Även om gyllene snittet kan tillämpas på oändligt olika sätt, så har man som fotograf lättast att tillämpa Fibonaccis teorier. 3:je dels regeln kommer från Fibonaccis.
2/1=2
3/2=1,5 Tredjedelsregeln
5/3=1,6667
8/5=1,60
13/8=1,625
(13+8)/13=21/13=1,615
.
.
233/144=1,618
.
.
Ju längre man fortsätter i talserien, ju närmare kommer man det gyllene förhållandet φ
φ=(1+√5)/2=1,61803398874989484820...
vilket är ett irrationellt tal... (Decimalerna fortsätter i oändlighet utan mönster...) och egentligen går det inte att beskriva exakt med rationella tal. Fibonaccis talserie kommer dock mycket nära!
Här följer en figur som illustrerar tillämpningen Fibonaccis delningar på en bild med 4:3 förhållande, fortfarande det vanligast förekommande vad gäller stillbildskameror.
http://www.fotosidan.se/gallery/viewlarge.htm?ID=1889705&target=_blank
Det går dock lika bra att tillämpa på vilka format som helst... 16:9 (HD-TV), 16:10 (Numer vanligare än 4:3 till datorer), 3:2 (standard fotopapper), (1+√2):2 (Standardpapper som A4 etc)
och utan att förminska betydelsen av alla de tusen format som förekommer, (1+√5):2 (Gyllene rektangeln).
Fibonaccis delningsregler är dock en grov förenkling av gyllne snittet, vilken även beskriver objekts uppbyggnad eller interna förhållanden. Av linjer bygger man rektanglar, vilka vidare beskriver spiraler. Gyllene snittet tillämpas även med vinklar, stjärnor (pentagram). Just som fotograf har man kanske lite svårt styra över hur objekten på bilden är uppbyggda, såvida man inte komponerar objekt efter ett visst mönster då, eller finner ett befintligt mönster att föreviga. Fibonaccis delningsregler anses dock särdeles effektiva då man beskär en bild, om man vill uppnå harmoni i en bild... Det som händer, eller blickfånget, ska vara i bildens gyllene snitt, ett av de fyra möjliga skärningspunkter delningsreglerna anger...
Lite länkar:
http://sv.wikipedia.org/wiki/Gyllene_snittet
http://en.wikipedia.org/wiki/File:Vector_Video_Standards2.svg
http://en.wikipedia.org/wiki/Paper_size
En mycket bra matematiskt förklaring. Jag har sammanställt lite information om gyllene snittet på min hemsida med exempel foton, då är det kanske enklare att förstå :-)
http://lahn.nu/fotografitips/gyllene-snittet/
Mvh Daniel