Fototeknik
Att verkligen förstå ett polarisationsfilter är mer komplicerat än man kan tro. Min förhoppning är att ändå försöka räta ut eventuella frågetecken.
Först måste vi reda ut begreppet ljus lite. Ljus karaktäriseras av våglängd och polarisation.
Våglängd
Till skillnad från till exempel ljudvågor som behöver ett medium ( t.ex. vatten eller luft) att utbreda sig i så kan ljus utbreda sig i vakuum. Ljus är elektromagnetisk strålning vilket innebär att det består av ett elektriskt och ett magnetiskt fält. Elektromagnetiska vågor är transversella vilket innebär att det elektriska och magnetiska fälten är vinkelräta mot utbredningsriktningen. Eftersom det elektriska och magnetiska fälten hänger ihop (det elektriska fältet i en utbredande våg kan inte existera utan det magnetiska fältet) och är ortogonala (vinkelräta mot varandra) så räcker det att vi diskuterar det elektriska fältet. Våglängden är avståndet mellan topparna i det elektriska fältet i fig. 3. Detta kan liknas med avståndet mellan topparna på vattenvågor.
Människoögat klarar att se våglängder mellan 3900Å och 7700Å (Å=Ångström = 10-10m). Ögats känlighet är som störst vid 5500Å (gul/grönt ljus). De korta våglängderna uppfattas som blå/blåviolett och de långa som rött. Kortare våglängder än 3900Å kallas ultraviolett ljus och längre än 7700Å kallas infrarött ljus. Vi kan inte uppfatta elektromagnetisk strålning med dessa våglängder men det är inte uteslutet att vår kamera gör det.
Vitt ljus består av en blandning av alla våglängder mellan 3900 och 7700Å. Man kan dela upp ljuset i sina våglängdskomponenter med ett prisma eller filter. Ett rödfilter släpper igenom de röda våglängderna av det vita ljuset men absorberar de blå våglängderna. Ett blått filter gör tvärtom. Om du sätter ett blått och rött filter efter varandra släpps inget ljus igenom.
Polarisation
Nästa viktiga begrepp är polarisation. Om det elektriska fältets vektor hela tiden ligger i ett plan kallas vågen linjärpolariserad.

Fig. 1
Ljuset på bilden har en våglängd och är linjärpolariserad. Polarisationsplanet definieras av det elektriska fältet som i bilden illustreras av de röda pilarna. Om man tar t.ex. en glödlampa så sänder den ut ljus med en massa våglängder och i många polarisationsplan (opolariserat). Glödlampsljuset kan beskrivas som en många komponenter av det som ses på bilden sammanslaget i en oändlig röra. Från denna röra kan man med hjälp av filter plocka ut de komponenter man är intresserad av. Med färgade filter kan man välja ut vissa våglängdsområden och med hjälp av polarisationsfilter kan man plocka ut den polarisation man är intresserad av.
Polarisationsfiltret
Polarisationsfiltret är som ett galler för ljus som bara släpper igenom ljus i en polarisationsriktning. Man kan tänka sig det som ett galler till en utegrill som bara släpper igenom pinnar som ligger längs gallret. Om ljuset har en polarisationsriktning som är 45 grader i förhållande till gallret så släpps ändå hälften av ljuset igenom eftersom ljusets elektriska fält är en vektor som kan delas upp i en komponent som är längs gallret, som släpps igenom, och en som är vinkelrät mot gallret, som stoppas.
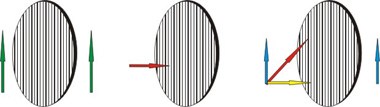
Fig. 2
I första fallet är ljusets polarisationsriktning längs filtret och allt ljus släpps igenom. I andra fallet är ljusets polarisationsriktning vinkelrät mot filtret och inget ljus släpps igenom. I tredje fallet är ljusets polarisationsriktning 45 grader i förhållande till filtret och hälften av ljuset släpps igenom.
Nu kan man undra vad detta har med fotografering och göra. Om man tar en normal ljuskälla som lampa eller solen så har ljuset ingen speciell polarisationsriktning utan är vad man kallar opolariserad. Det enda som då händer om man sätter ett polarisationsfilter framför objektivet är att hälften av ljuset inte släpps igenom polarisationsfiltret och man tappar ett bländarsteg i ljusstyrka ( I praktiken dämpar polarisationsfiltret ytterligare så att man tappar upp 0,5 - 1 bländarsteg till).
Men det finns två fall där ljuset inte är opolariserat, det ena är efter en reflektion mot en dielektrisk yta och det andra är ljuset från en blå himmel.
Polarisation genom reflektion
När ljuset träffar ett dielektriskt material (t.ex. plast, glas eller vatten) så reflekteras en del av ljuset av materialet. Vi brukar säga att materialet är blankt. Det ljus som faller in snett mot materialet kommer att reflekteras nästan helt polariserat. Ljus som faller in vinkelrätt mot materialet kommer dock att reflekteras opolariserat. Vid en viss infallsvinkel, som kallas Brewster-vinkeln, kommer det reflekterade ljuset att vara helt polariserat. Det ljuset som reflekteras har sitt polarisationsplan längs den reflekterade ytan.
I praktiken innbär detta att ett polarisationsfilter har ingen inverkan om du fotar vinkelrätt genom en fönsterruta men däremot undertrycks reflexioner i fönstret om du fotar snett genom fönstret om du vrider polarisationsfiltret till rätt läge, d.v.s. så att polarisationsfiltrets "galler" är vinkelrätt mot det reflekterade ljusets polarisationsplan.
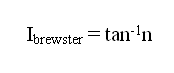
där n=det dielektriska materialets brytningsindex
För vatten är brytningsindex 1,33 och Brewstervinkeln blir 52 °.
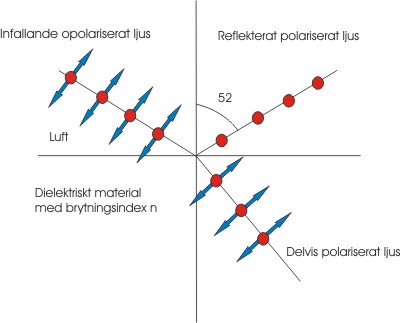
Fig. 3
Det går att beräkna reflektion mot t.ex. en vattenyta även för andra infallsvinklar och då ser kurvorna för reflektion ut så här. Den reflekterade vinkeln är lika stor som infallsvinkeln.
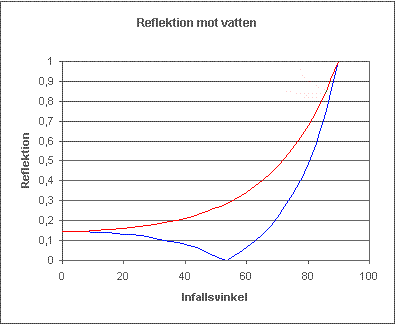
Fig. 4
Den röda kurvan motsvarar den "röda" polarisationen i fig. 3 och motsvarande för den blå kurvan.
Som synes reflekteras endast den röda polarisationen vid 52 garaders infallsvinkel och man kan då med ett polarisationsfilter filtrera bort den reflekterande polarisationen. Vid 0 och 90 graders infallsvinkel reflekeras båda polarisationerna lika mycket varför polarisationsfiltret då inte har någon verkan. Däremellan gör den viss verkan men mest vid Brewstervinkeln som i detta fall är 52 grader.
Som exempel har jag tagit kort på en bok igenom en glasskiva med kraftiga reflektioner från ett fönster.

Fig. 5
Utan polarisationsfilter

Fig. 6
Med polarisationsfilter i vertikal riktning.
Som synes gör polarisationsfiltret mest nytta mitt i bilden. Högst upp avviker reflexionsvinkeln mer från Brewstervinkeln och effekten blir sämre.
Olika glassorter har brytningsindex mellan 1,44 - 1,9 varför Brewstervinkeln är mellan 55 - 62 grader. För plaster varierar brytningsindex mellan 1,45 - 1,7 och Brewstervinkeln mellan 55 - 60 grader.
Observera att fenomenet ej gäller för metaller.
Polarisation genom spridning
När ljuset från solen passerar var atmosfär träffar ljuset på luftmolekyler i luften. När ljuset "krockar" med luftens molekyler reflekeras en del av ljuset mot dessa. Korta våglängder reflekteras mer än långa. Detta kallas Rayleigh-spridning. Om inget ljus skulle spridas mot luftens molekyler skulle himlen vara svart vid klar himmel. Det reflekterade ljuset kommer att vara delvis polariserat. Ett enkelt experiment för att studera detta fenomen är att blanda några droppar mjölk i ett glas med vatten och sedan belysa lösningen med en ficklampa. Det ser då ut så här.

Fig. 7
Som man kan se så syns det ett blåaktigt ljus till vänster där ljuset kommer in. Det beror på att när ljuset från ficklampan träffer partiklar i lösningen så sprids ljuset av dessa men det är framförallt det blå ljuset som sprids. Tittar vi till höger så har det mesta av det blå ljuset gått förlorat så att man ser när det gula ljuset sprids. Av samma skäl är himlen blå på dagen. På kvällen när solen står nära horisonten så går solljuset mycket längre väg genom atmosfären så att det blå ljuset redan har "filtrerats" bort innan ljuset når oss varför himlen bli gul/röd.
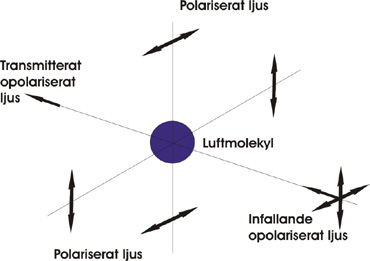
Fig. 8
Eftersom ljuset som sprids är polariserat så går det att påverka med ett polarisationsfilter. Om vi antar att ljuset är helt polariserat så skulle du kunna ställa in ditt polarisationsfilter så att inget ljus från himlen når filmen/CCD´n och himlen skulle i så fall bli helt svart på bilden.
Så här kan det se ut i verkligheten.

Fig. 9
Utan polarisationsfilter. Solen från sidan.

Fig. 10
Med polarisationsfilter. Solen från sidan.
Eftersom det blå blir mörkare framträder molnen bättre.
Om man har solen i ryggen blir inte effekten så stor.

Fig. 11
Utan polarisationsfilter. Solen i ryggen.

Fig. 12
Med poarisationsfilter. Solen i ryggen.
Skillnaden i den blå himlen är mindre nu. Däremot syns det stor skillnad på reflexionerna från löven trädet .
Cirkulära/linjära polarisationsfilter
Om man tittar i en prislista hos en fotohandlare så ser man att det finns både linjära och cirkulära polarisationsfilter. Anledningen till att det finns cirkulära är att vissa kamerors strålgångsmätning (fråga mig inte vilka) inte fungerar så bra med vanligt polarisationsfilter. Strålgångsprismat som delar upp ljuset mellan sökarbilden och strålmätningssystemet behöver opolariserat ljus för att fungera bra. . Det ordnar man genom att omvandla den linjära polarisationen från ett polarisationsfilter till cirkulärpolariserat ljus som har polarisationsplan i alla riktningar precis som opolariserat ljus. Ett cirkularpolariserat filter består således av två skikt, ett skikt som är polarisationsfilter och ett som omvandlar linjär polarisation till cirkulär polarisation. Diskussionen ovan gäller således både för linjära som cirkulära polarisationsfilter. Ett cirkulärt polarisationsfilter har alltså samma egenskaper som ett linjärt polarisationsfilter.

Fig. 13
Cirkulär polarisation kan beskrivas som två stycken linjära vågor som är vinkelräta och fasförskjutna 90 grader i förhållande till varandra. Cirkulär polarisation kan åstadkommas från en linjär våg genom att fördröja komponenten 45 grader från den linjära vågen 90 grader. Som synes i Fig. 13 får man då ett polarisationsplan som roterar i tiden.
Som jag skrev i början är det ett komplicerat ämne. Jag hoppas att artikeln ger alla något, oavsett förkunskaper.
MVH/ Torsten





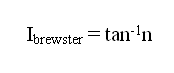































33 Kommentarer
Logga in för att kommentera
Kul experiment du hittat på Fredric. Och visst ska det bli så om man betraktar polarisationsplanet som en vektor som kan delas upp i komponenter som ligger längs "gallret" respektive vinkelrätt mot "gallret".
Det enda jag inte förstår är varför det står att det är 12 röster längst uppe till höger när jag bara ser 7?
en liten undrar dock. Varför hålla sig till Ångström som längdenhet. Varför inte SI-enhet? Det är vad man får lära sig numera...
Som Linus frågar om enheten så är det normalt att använda nanometer (10-9) för att beskriva våglängderna, vidare så är beteckningen "osynlilgt ljus" inte korrekt men används tyvärr till vardags, det handlar ju om UV-eneri respektive Infraröd energi då det ligger utaför det synliga spektrat. Tänk om vi skulle säga "osynligt men hörbart ljus" om våglängder som vi normalt benämner som "ljud".
Nu när vi har några svenska forskare som lyckats sätta sina namn på enheter tycker jag om att vara patriotisk och använda enheter namngivna efter dom.
Därför brukar jag använda Ångström för våglängd och Celsius för temperatur fast SI-enheterna är nanometer respektive Kelvin..;)
En annan mycket mindre petig sak är att ett pol.filter i 45 graders vinkel teoretisk släpper igenom ca 70% av ljuset men det är inte så noga med det. Totalt så snor mitt eget filter ungefär 50% av opolariserat ljus.
Bara lite småsaker. Väldigt bra artikel ändå. Det brukar inte vara så lätt att förklara sånt här. Jag vet :) men jag tycker du lyckats bra.
/Fredrik
Det är riktigt att 70% av amplituden släpps igenom (sin(45°)=0,707=70,7%) men ljusstyrkan är proportionell mot amplituden i kvadrat (sin(45°)²)=0,5=50%)
Det kanske var slarvigt av mig att skriva ljuset i stället för ljusstyrkan men det är ju ljusstyrkan som räknas i sådana här sammanhang).
En fotons energi är frekvensen * h (boltzmanns konstant, ett uttefjuttigt litet tal för övrigt)
Så långt inte så konstigt. Kruxet är bara det att antingen fastnar elektronen i polarisationsfiltret eller också gör den det inte. Bara en del av "amplituden" kan inte fastna. Fotonen måste helt enkelt välja om den ska fastna eller inte. Detta går till så att ljuset helt enkelt polariseras om så att det antingen blir polariserat 90 grader mot filtret eller 0 grader mot (dvs med) filtret. Formeln för intensiteten bakom filtret lyder I=I0*cos(v)^2 och v=45 grader ger då I=I0*0.5
Det är för övrigt av samma anledning man kan få ljus att passera genom två vinkelrät ställda polarisationsfilter genom att placera ett tredje emellan. Om man tex placerar det tredje i 45 graders vinkel jämfört med dom andra kommer ljuset att vara polariserat 45 grader jämfört med mittenfiltret som sedan kommer att polarisera om det i sin egen polarisationriktning dvs 45 grader mot det tredje filtret som då alltså helt plötsligt kan släppa igenom hälften av ljuset. Totalt kommer alltså 25% av ljuset som passerade det första filtret att komma ut efter det tredje.
Magi och trolleri men det är faktiskt så det funkar. Resonemanget med amplituder fungerar dock bra med avseende på vattenvågor och dylikt.
Hoppas att jag i och med detta inte blir bannlyst från all fortsatt inblandning i fotosidan.
/Fredrik
Fredrik: Jag begriper inte riktigt vart du vill komma. Orsaken till att man utgår från ljusstyrkan (intensiteten) i dessa sammanhang beror på att en detektor (t ex ögat) inte uppfattar ljusets snabba växlingar utan registrerar den absorberade energin under ett visst ändligt tidsintervall. Denna intensitet är proportionell mot tidsmedelvärdet av amplituden i kvadrat. Därför betraktar man ljusets intensitet. En annan orsak är att ljuset i fotografisammanhang är inkoherent, varför amplitudbegreppet inte är intressant.
Och jag som verkligen trodde jag var smart..
Men men, man kan nog vara smart på flera olika sätt ;)
Energin för fotonen beräknas som sagts med sambandet E = h * f, men h är Plancks konstant och ingen annans. Värdet är mycket riktigt väldigt litet h=6*10^-34 Js. (Boltzmanns konstant är mycket större och har dessutom en annan enhet som inte duger här.)
Ett sånt ska jag ha.
(Bara för att vara lite duktig)
Med vänlig hälsning Johan
Jag förstår hur jag menar, frågan är.. förstår du hur jag menar? :P
Peter: man snurrar på det för att kunna filtrera bort ljuset från olika vinklar. Testa på kvällen, titta genom sökaren på ett fönster som reflekterar en datorskärmen/tv (datorkärmen/tv:n står i samma rum som dig mao). Prova att vrida på filtret så skall du se vad som händer. Anledningen till att den helt plötsligt blir svart är att polfiltret filtrerar bort ljuset i den vinkeln.
Jag har med stort intresse läst din artikel om polarisationsfilter. mycket pedagogiskt! Det mesta är klart, men det finns en sak jag inte förstår.
Givet alla förutsättningar du anger, hur kommer det sig att himlen blir blåare, att kontrasten ökar i färgerna, med hjälp av filtret? Eftersom det i atmosfären reflekterade blå ljuset p.g.a. våglängden sprids mer, borde funktionen var omvänd: med polfiltret kan jag filtrera bort det polariserade, blåa ljuset och färgmättnaden borde på så vis minska.
Var tänker jag fel?